9 Hypothesis Testing - An Introduction 9.3 Direction of Extreme - To the Right 9.5 Simulations

9.4 Direction of Extreme - Two Sided

Example: Suppose that two populations of numbers are as follows: Population 1 contains one -3, two -2s, three -1s, four 0s, three 1s, two 2s, and one 3; Population 2 contains four -3s, three -2s, two -1s, one 0, two 1s, three 2s, and four 3s. Figure 9.8 illustrates.

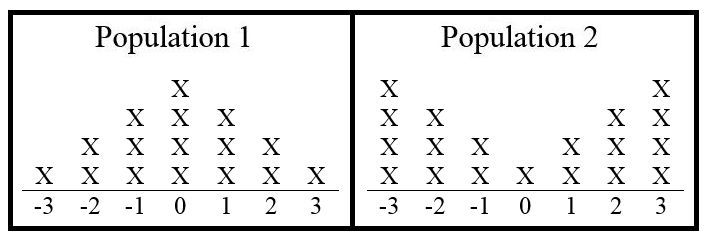
Suppose a box is chosen, and a number from the box is chosen at random. The hypotheses for this test are:

\begin{array}[]{ll}H_{0}:&\mbox{The sample came from Box 1.}\\ H_{1}:&\mbox{The sample came from Box 2.}\\ \end{array}

Note that stronger evidence against $H_{0}$ are values that are large or values that are small. In this case we call the direction of extreme two sided. For example, 3 and -3 give the same level of evidence against $H_{0}.$ If a 3 is the selected number, then the corresponding $p$ -value is $2/16=0.125,$ because there are a total of 16 numbers in Box 1 (remember that $H_{0}$ is assumed true), and 3 and -3 are the only numbers at or more extreme than the selected 3. Figure 9.9 illustrates.

Figure 9.9: $p$ -value if 3 is Seclected

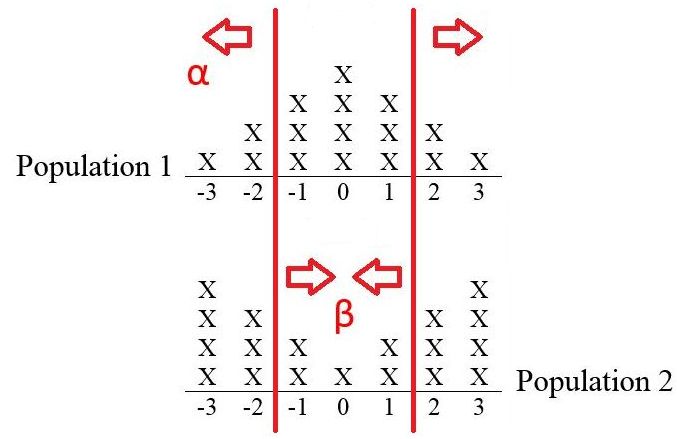
Similarly, computations for $\alpha$ and $\beta$ are done using symmetry as well. For example, if the decision rule is “reject $H_{0}$ if the observed number is $\pm 2,$ or more extreme,” then $\alpha=6/16=0.375$ and $\beta=5/19\approx 0.2632.$ Figure 9.10 illustrates.

Figure 9.10: Two-sided $\alpha$ and $\beta$

Concepts Check:

1.

Suppose that the selected voucher is 1. What is the corresponding $p$ -value?
Answer: $12/16=0.75$
2.

Suppose that the decision rule is “reject $H_{0}$ if the selected number is $\pm 3,$ or more extreme.” What is the value of $\alpha?$
Answer: $2/16=0.125$
3.

Suppose that the decision rule is “reject $H_{0}$ if the selected number is $\pm 3,$ or more extreme.” What is the value of $\beta?$
Answer: $11/19\approx 0.5789$