9.3 Direction of Extreme - To the Right

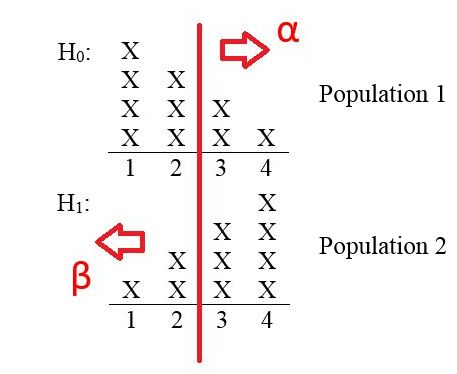
Example: Suppose that two populations consist of numbers as follows: Population 1 contains four 1’s, three 2’s, two 3’s, and one 4; Population 2 contains one 1, two 2’s, three 3’s, and four 4’s. Figure 9.5 illustrates.

A population is selected at random, and then a random sample of size 1 is chosen from the selected population. Using the sample chosen, a decision is to be made on the following hypotheses:

Note that the direction of extreme is to the right, i.e., the larger the number selected, the stronger the evidence against $H_0.$ As in the prior example, since the sample is of size one, the test statistic can be the number (1, 2, 3, or 4) selected. We will do that again.

In performing the hypothesis test, suppose the significance level is $\alpha =\mathrm{0.3.}$ This choice would make 3 the critical value, because there are three out of ten numbers in Population 1 that are 3 or greater. Similarly, the rejection region is values 3 or greater, because of the choice of $\alpha$ and the direction of extreme. The value of $\beta$ is also $3/10,$ as there are three numbers in Population 2 that are strictly smaller than 3. See Figure 9.6.

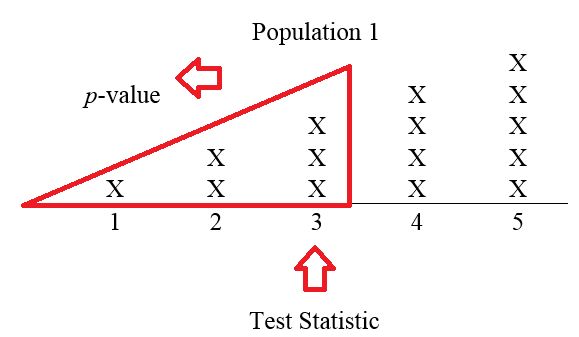
Suppose that the sample selected is the number 4. Then the corresponding $p$-value is 1/10, as there is just one number in Population 1 that is equal to or more extreme than 4. Since the $p$-value is , the null hypothesis, $H_0,$ is rejected. See Figure 9.7.

Since $H_0$ is rejected, a Type I error may have occurred. Note that upon rejecting $H_0,$ the probability of committing a Type I error is 0 (the error did not occur) or 1 (the error did occur).

Concepts Check

1. 1.

   True or false: If the direction of extreme is to the right, then larger values of the test statistic give stronger evidence against $H_0.$
   Answer: True

2. 2.

   If the number selected is 2, what is the corresponding $p$-value?
   Answer: $6/10=0.6$

3. 3.

   If the decision rule is “reject $H_0$ if the selected number is 4 or more,” what is the value of $\alpha \mathrm{?}$
   Answer: $1/10=0.1$

4. 4.

   If the decision rule is “reject $H_0$ if the selected number is 4 or more,” what is the value of $\beta \mathrm{?}$
   Answer: $6/10=0.6$

Remark: This example illustrates an important relationship between $\alpha$ and $\beta :$ If $H_0$ is false, then the smaller your choice of $\alpha ,$ the more likely a Type II error will occur. Equivalently, if $H_0$ is true, the smaller the value of $\beta ,$ the more likely a Type I error will occur.