5 Algorithmic Thinking

5.6 Lists

Goals:
∙ Learn how to create lists in Python;
∙ Learn how to manipulate lists.

A data structure is a way of organizing data. For our purposes, we will work with one type of data structure in Python, namely lists. In Python, a list is a finite sequence of things, separated by commas, beginning and ending with brackets [ and ], respectively. For example, [3, 6, 3, 5, -1] is a list. In a list, order and location matter. For example, the following lists are all different: [2], [2, 2], [2, 3], [3, 2].

An element in a list is located by its index. The first index is 0, and the index increases by 1 for each element as you scan from left to right. For example, in the list [3, 6, -2], element 3 has index 0, 6 has index 1, and -2 has index 2. In Python, to access the value with index i in a list L, the syntax is L[i]. For example, suppose L = [3, 4, 1, 5, -3, 9]. Then L[0] returns 3, while L[2] returns 1.

The number of elements in a list is its length. For example, [9,9] has length 2, while [[1, 2], 3, -4] has length 3. A useful function, called len, returns the length of a given list. For example, if L = [3, 4, 1, 5, -3, 9], then len(L) returns 6. The function len is a key function for working through elements of a list.

Example 5.6.1.

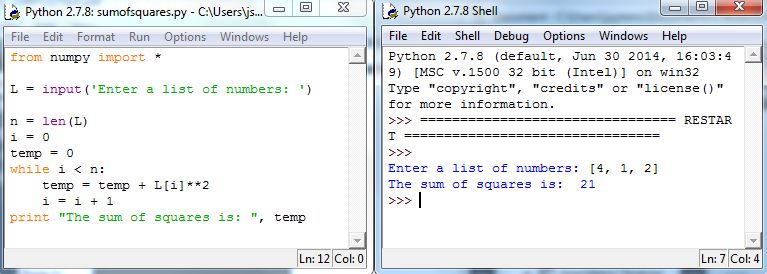
Compute the sum of squares of a list of numbers [x1,x2,…,xn], i.e., compute

∑i=1nxi2=x12+x22+⋯+xn2.

Solution. Because we can compute the length of a list, we can use a while loop to build the sum, terminating once the list of elements is traversed:

PythonCommentsL = input('Enter a list of numbers: ')input a listn = len(L)compute the length of Li = 0initialize the indextmp = 0temp will store the sumwhile i < n:loop to build the sum    temp = temp + L[i]**2add the square to temp    i = i + 1bump the index upprint "The sum of squares is: ", tempoutput the sum

Note that in the loop the last iteration of the loop occurs when i=n-1, the index of the last element in the list; when i gets bumped up to n, the loop terminates. Figure 5.18 shows the code in action:

Figure 5.18: Sum of Squares Code

♣

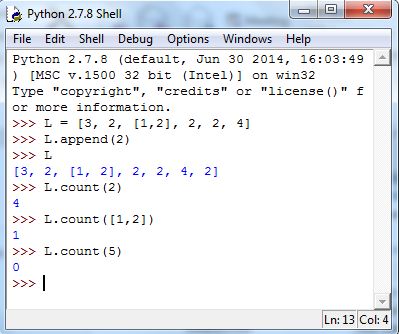
Lists have built in functions, called methods. We’ll make use of two, namely append and count. Here’s how each works: Suppose L is the name of a list stored in Python’s memory, then:

  • •

    L.append(x) appends x to the end of list L;

  • •

    L.count(x) returns the number of times x is in list L.

Figure 5.19 provides examples of using the two methods:

Figure 5.19: List methods append and count
Example 5.6.2.

Suppose we have a 4-sided die with faces marked as 1, 2, 3, and 4. And, suppose that if in rolling the die, the chance of rolling one of the numbers is given by the following discrete distribution:

RollProbability11/521/532/541/5

Suppose the die is rolled twice, what is the probability that the two rolls sum to 5?

Solution. We can approximate an answer using a simulation, using a list to store the simulated data.

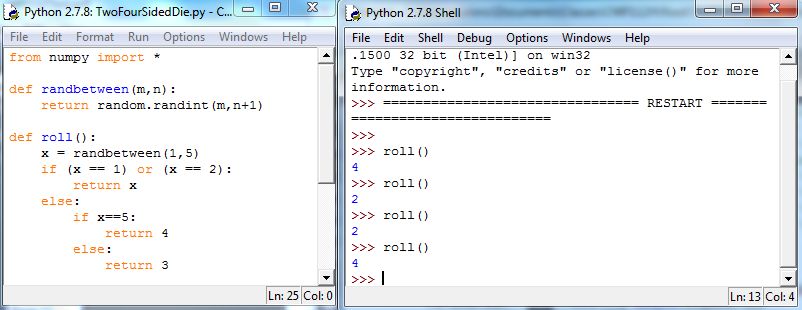
Using randbetween(1,5), we can simulate rolling the die once by declaring:

randbetween(1,5)Resulting Roll1122334354

To simplify the problem, we can define a function, say roll, that simulates rolling a single die. Then executing roll() + roll() will simulate rolling twice and computing the sum. Appending these results to a list will build a simulated sample, and from that we can compute the sample proportion of 5’s. Here’s the code for roll:

PythonComments x = randbetween(1,5):    if (x == 1) or (x == 2):is x equal to 1 or 2?        return x:x is equal to 1 or 2    else:x isn’t 1 or 2        if x == 5:is x equal to 5?            return 4x is 5        else:x is 3 or 4            return 3

Figure 5.20 shows roll in action:

Figure 5.20: Rolling an Unfair 4-Sided Die

Code that will iterate roll() + roll() can be written as follows:

PythonComments def go(n):n = number of iterations    i = 1initialize the counter    L = []initialize the list    while i <= n:stop the loop when i > n        x = roll() + roll()simulate two rolls and add        L.append(x)append the result to L        i = i + 1bump the counter    return Lreturn the sample

Figure 5.21 illustrates:

Figure 5.21: Simulated Samples

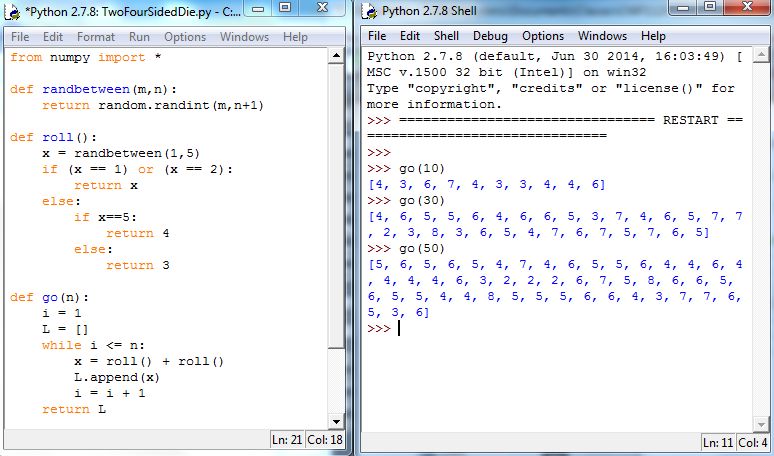
Lastly, we need to count the number of 5’s in a sample and divide by the sample size. We can do that with the following command:

L.count(5)float(len(L)).

(Recall that float will convert the integer into a floating-point number.) Adjusting the return line in go will yield results as shown in Figure 5.22.

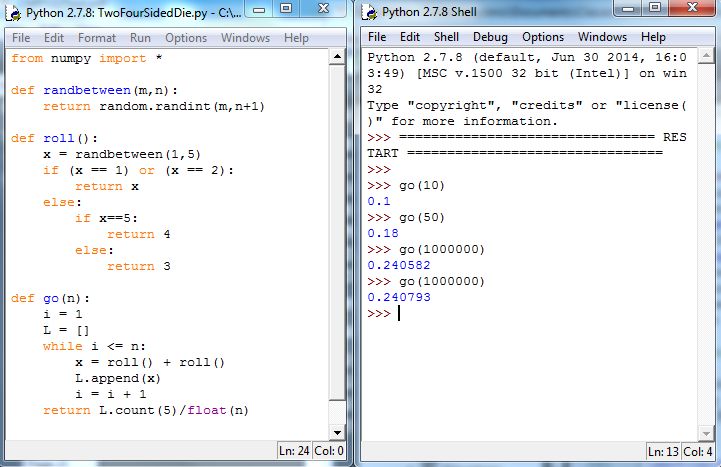
Figure 5.22: Simulated Proportions of 5’s Rolled

♣


Concepts Check: 1. Based on the output in Figure 5.22, what would you estimate as the probability of getting a 5? Answer: ≈0.240 2. What is the output of the command [3, -1, 4, 2, 99][3]? Answer: 2 3. What is output to the command [3, -1, 4, 2, 99].append(3)? Answer: [3, -1, 4, 2, 99, 3]

5.6.1 Exercises

  1. 1.

    What is the output of the following code:

    L = [4, 2, 7, 8]i = 1temp = 0while i < 3:    temp = temp + L[i]    i = i + 1print temp
  2. 2.

    Without using a library, such as numpy, write a function that takes as input a list of numbers, and outputs their mean. Compare your output to the output of the numpy function mean.

  3. 3.

    Write a function that takes as input a list, and outputs a list with elements listed in the opposite order.