5.1 An Interactive Calculator

Because installations of Python vary from year to year, we assume in this text that your instructor has shown you how to start Python, whether you are in a traditional classroom or online course.

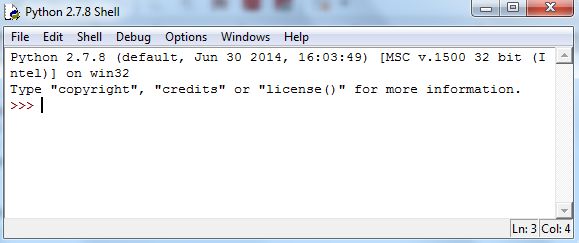
Open Python. Depending on the setup, you will have one or two windows. Select the window labelled as Python Shell. It will look like Figure 5.1.

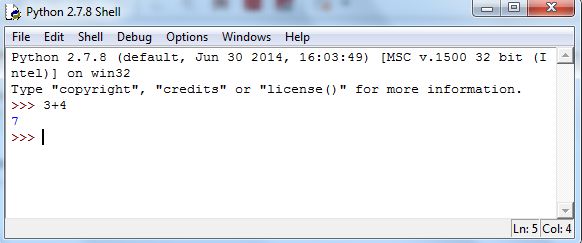
At the >>> prompt, type in some arithmetic expression, such as $3+4,$ and then hit Enter. When you hit Enter, Python will attempt to process whatever you’ve typed. Figure 5.2 contains the result.

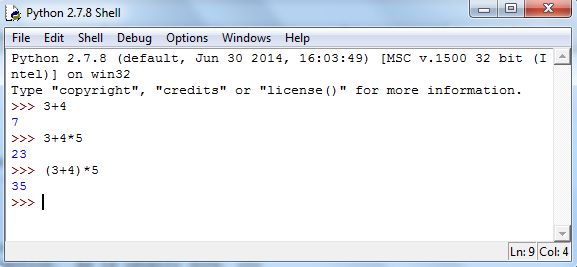
Addition, subtraction, multiplication, and parentheses work in Python as in Excel. Try computing $3+4\cdot 5$ and $(3+4)\cdot 5$ in the Shell. You should see Figure 5.3.

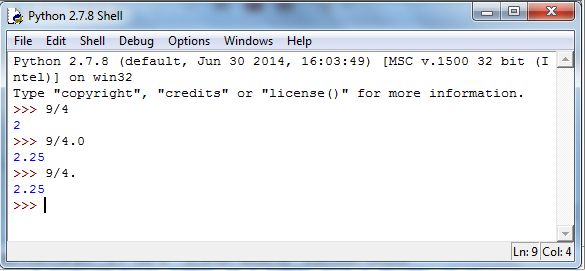
Division and exponentiation, however, are both different in Python. If $x$ and $y$ are integers, x/y will compute the quotient of $x$ divided by $y.$¹⁶¹⁶Henceforth, Python commands will be displayed using this font. For example, try 9/4 in the Shell, and you’ll get 2. To get a floating-point approximation to $x/y,$ one of the two needs to be a floating-point number.¹⁷¹⁷You can think of a floating-point number as a number with a decimal in it. The simplest option is to type 9/4.0, and you’ll get 2.25. Figure 5.4 demonstrates.

To compute $x^y$ in Python, type x**y. Figure 5.5 demonstrates $2^8.$ Be careful, 2$\widehat{}$8 does something different (note the output).

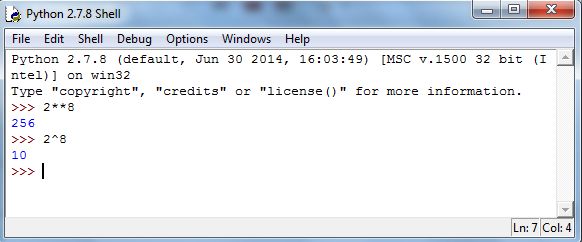
Two examples:

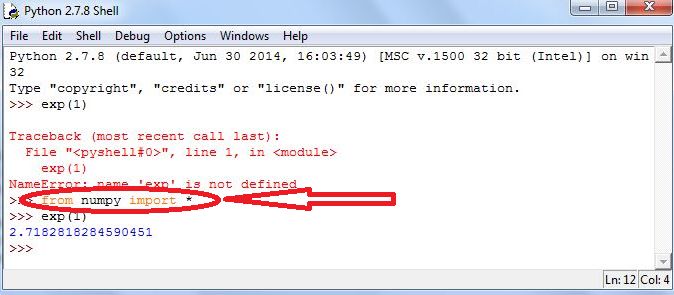
We you start Python, a minimal number of commands are automatically loaded. For example, you will recall the exponential function of base $e,$ $f(x)=e^x.$ As with Excel, this function is called using exp(). But, before calling the function, we need to load it. Try executing exp(1) in Python and you will get an unsightly error. There is a large number of libraries of commands for Python, and we will rely on the one named numpy. This library contains many definitions of functions for working with numbers, including the familiar functions on a scientific calculator. The following command will load the library:

Now try exp(1) again and you’ll see an approximation to the number $e,$ as in Figure 5.6.

A note: Recall that logarithms are the inverse functions to exponential functions. The natural logarithm function is the inverse function of exp. The most common mathematics notations for the natural logarithm function are $\ln ,$ ${\log }_e$ and $\log .$ The numpy library uses log. To see this, execute log(exp(4)).

Some examples using commands from numpy:

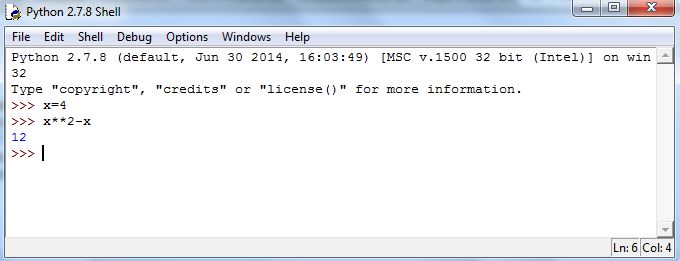
Another way we can use Python like a standard calculator is with storing numbers. But, with Python we can do so more elegantly, and with greater power. We can assign values to variables in Python, and then compute with them symbolically. To assign a value, we use the equal sign, =. For example, executing x = 4 will store the value of 4 into x. (We’ll discuss naming things as we develop examples.) Then executing x**2 - x will yield the correct value, as shown in Figure 5.7.

1. 1.

   Answer the following as True or False.

   1. (a)

      The module numpy is needed to use the command exp.

   2. (b)

      If we wanted to square the value of 2, we would type 2$\mathrm{\wedge }$2.

   3. (c)

      If we typed 2/2 in Python, the value of 0 would be produced.

   4. (d)

      Addition and subtraction symbols are exactly the same as that in Excel.

   5. (e)

      The command for square root in Python is sqrt.

2. 2.

   Store $x=9$ and $y=12$ and $z=-3$. Compute the following.

   1. (a)

      ${(x-3)}^2+{(y-4)}^4-{(z+3)}^8$

   2. (b)

      $(x/y)-z$

   3. (c)

      ${\displaystyle \frac{x-y+z}{z^2+x^2}}$

   4. (d)

      $\exp (z)-\sin (xy)$