9 Hypothesis Testing - An Introduction 9.6 Chapter Summary 10 Testing a Single Population Mean

9.7 Exercises

1.
Write out $H_{0}$ and $H_{1}$ for the following scenarios.
1. (a)
  
  A tire manufacturer claims that their tires last for an average of 50,000 miles. We think that claim is too high.
2. (b)
  
  An ad in the college newspaper claims that the average rent for a two-bedroom apartment near campus is $750 per month. We think that claim is too low.
3. (c)
  
  A headache medicine claims that its time to relief is thirty minutes. We want to see if that claim is accurate.
4. (d)
  
  While grading final exams, a physics professor gets the feeling that scores are lower than normal (80%) this semester. She decides to test that feeling empirically.
2.

Two identical-looking populations contain numbers as shown in Figure 9.22.

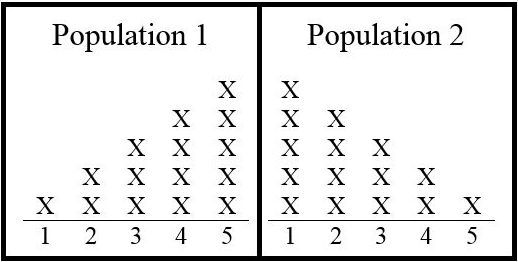
Figure 9.22: Population 1 & 2
One of the populations is selected, and a single number is selected. The competing hypotheses are:
1. $H_{0}:$ The number was selected from Population 1.
2. $H_{1}:$ The number was selected from Population 2.
3. (a)
  
  What is the direction of extreme? To the left, to the right, or two sided?
4. (b)
  A significance level of 0.2 is chosen.
  1. i.
    
    What is the critical value?
  2. ii.
    
    What is the corresponding value of $\beta?$
5. (c)
  Suppose that from the selected population, a 1 is chosen.
  1. i.
    
    What is the $p$ -value?
  2. ii.
    
    If $\alpha=0.2,$ what decision is made?
  3. iii.
    
    What error might have occurred, Type I or Type II?
3.

Two populations consist of numbers as shown in Figure 9.23.

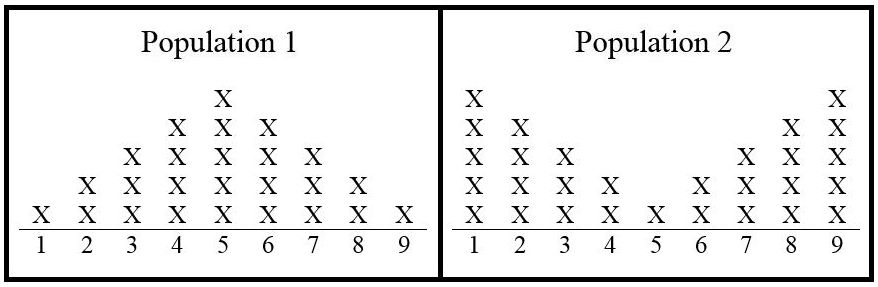
Figure 9.23: Populations 1 & 2
One of the populations is selected, and a single number is randomly selected. The competing hypotheses are:
1. $H_{0}:$ The number was selected from Population 1.
2. $H_{1}:$ The number was selected from Population 2.
3. (a)
  
  What is the direction of extreme? To the left, to the right, or two sided?
4. (b)
  
  A significance level of 0.08 is chosen. What is the corresponding value of $\beta?$
5. (c)
  Suppose that from the selected population a 9 is chosen.
  1. i.
    
    What is the $p$ -value?
  2. ii.
    
    If $\alpha=0.08,$ what decision is made?
  3. iii.
    
    What error might have occurred, Type I or Type II?
6. (d)
  
  Suppose that from the selected population a 3 is selected. What is the corresponding $p$ -value?
4.

Two populations contain numbers as shown in Figure 9.24.

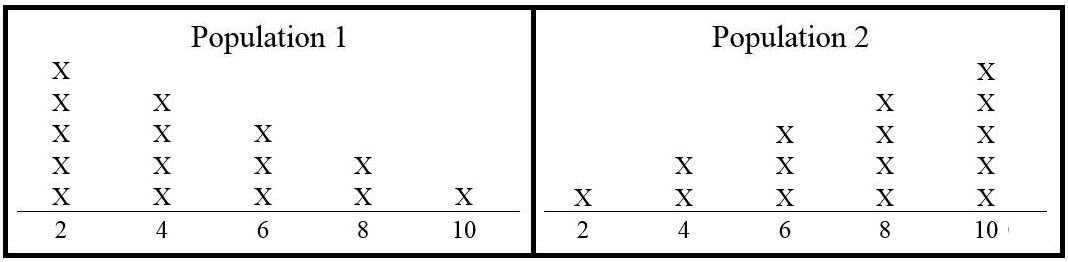
Figure 9.24: Populations 1 & 2
One of the populations is selected, and a single number is selected. The competing hypotheses are:
1. $H_{0}:$ The number was selected from Population 1.
2. $H_{1}:$ The number was selected from Population 2.
3. (a)
  
  What is the direction of extreme? To the left, to the right, or two sided?
4. (b)
  The decision rule is “reject $H_{0}$ if the selected number is 8 or more extreme.”
  1. i.
    
    What is the corresponding value of $\alpha?$
  2. ii.
    
    What is the corresponding value of $\beta?$
  3. iii.
    
    Suppose that a 10 is chosen. What is the $p$ -value?
  4. iv.
    
    If a 10 is chosen, what is the decision, reject $H_{0}$ or fail to reject $H_{0}?$
  5. v.
    
    What error might have occurred, Type I or Type II?
5.
Using the populations and hypotheses given in problem 1, do a simulation in Excel of selecting a single number from a randomly selected population. Use a decision rule of “reject $H_{0}$ if the selected number is 2 or more extreme.”
1. (a)
  
  Check that the proportion of Type I errors that occur when $H_{0}$ is true is approximately equal to $\alpha.$
2. (b)
  
  Check that the proportion of Type II errors that occur when $H_{0}$ is false is approximately equal to $\beta.$
6.
Using the populations and hypotheses given in problem 1, do a simulation in Excel of selecting a sample of size 2 from a randomly selected population. Assume sampling with replacement. Use a decision rule of “reject $H_{0}$ if the sample mean is 2 or more extreme.”
1. (a)
  
  Approximate $\alpha$ by computing the proportion of Type I errors that occur when $H_{0}$ is true. Compare this value with the $\alpha$ in the prior problem.
2. (b)
  
  Approximate $\beta$ by computing the proportion of Type II errors that occur when $H_{0}$ is false. Compare this value with the $\beta$ in the prior problem.
7.

Using the populations and hypotheses given in problem 1, do a simulation in Excel of to estimate the $p$ -value if a sample mean of 2.0 is observed from a random sample of size 2.